In this article, principle, construction, working, voltage equation and torque equation of switched reluctance motor is given.

Principle of Switched Reluctance Motor

The working of switch reluctance motor is similar to that of variable reluctance stepper motor. The torque in the reluctance motor is generated such that inductance of stator winding becomes maximum.

Construction of Switched Reluctance Motor

The field winding of the motor is similar to that of DC Motor field winding whereas the rotor of the motor does not have any winding or permanent magnet on it.
As there are salient poles on both stator and rotor, it is also called as Double salient pole motor.
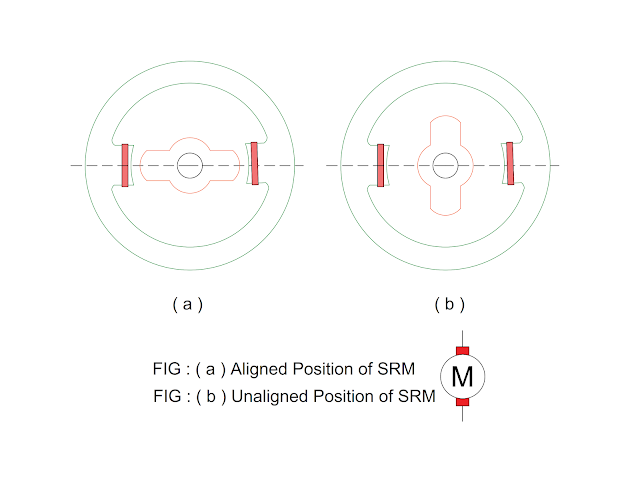
The 6/4 ( 6 poles on stator and 4 poles on rotor ) type switch reluctance motor is shown in the Figure.
The stator coils of N poles and S poles are connected in series.
The three-phase supply is given to stator winding through three phase converter.

Working of Switched Reluctance Motor

The rotation of rotor is done if the stator winding is energized sequence.
If the opposite polarity poles of stator winding is energized, the rotor always keep to maintain its position in minimum reluctance.
When two poles of rotor are aligned with opposite poles of stator, remaining poles of rotor does not aligned.
The rotation of rotor and torque depends upon stator winding current.

Aligned & Unaligned Position of Rotor

Figure shows the position of rotor with respect to stator.

( a ) Aligned

Rotor displacement angle at 0 degree or 180 degree
Maximum inductance between stator poles and rotor poles
Zero torque
Magnetic circuit may saturate
Stable operation

( b ) Unaligned

Rotor displacement angle at + 90 degree or – 90 degree
Minimum inductance between stator poles and rotor poles
Zero torque
Magnetic circuit does not saturate
Unstable operation

Variation of Inductance with Rotor Position

Figure shows the position of inductance of coil with respect to rotor.

Assumption

Constant current passes through stator coil
Effect of stator coil saturation and fringing is neglected
The stator coil inductance region is explained here.

Region 1 : 0 – θ_E’& θ_E – θ_E’

The stator and rotor poles do not overlap in this region.
The inductance becomes minimum and constant in this region so it does not produce any torque.

Region 2 : θ_E’– θ_A

The stator and rotor poles – aligned – in this region.
When the stator poles are aligned with rotor poles, the inductance increases.
The stator and rotor aligned position is shown in the figure.
The inductance increases in positive direction and positive motoring torque is generated.
When overlapping of stator and rotor poles comes to end, this region completed.

Region 3 : θ_A– θ_A’

The movement of rotor poles do not affect the overlapping between stator and rotor poles.
The torque does not generate in spite of maximum inductance and constant current passes through stator coil.
This is useful when the stator current comes to zero or low level when it is commutated.
Thus it prevents negative torque generation in the negative slop region of the inductance.

Region 4 : θ_A’– θ_E

When rotor moves forward to the overlapping region of stator in the clockwise direction, inductance decreases.
It produces negative torque therefore this mode of operation in the SRM is also called as generating mode.

When stator and rotor poles are separating each other, current is made zero in order to reduce negative torque in the SRM. The torque generated by one pulse is called as stroke.

Inductance Profile & Torque

Voltage Equation of Switched Reluctance Motor

The following assumption is made when deriving voltage equation of SRM.

Effect of magnetic saturation is neglected
Effect of fringing is neglected
Effect of mutual coupling between phases is neglected

The supply voltage is equal to sum of voltage drop in resistance and rate of change of flux

V = iR + ( dψ / dt )

= iR + [( dψ / dθ ) ( dθ / dt )]

= iR + ω_m ( dψ / dθ ) [ ⸫ ω_m = dθ / dt ]….. ( 1 )

Where

V = Supply voltage

i = Current

ψ = Flux Linkage

R = Resistance per phase

L = Inductance per phase

ω_m = Angular Speed

θ = Rotor position

Inductance L = Flux Linkage ( ψ ) / i ………… ( 2 )

From equation ( 1 ) and ( 2 )

V = iR + ω_m [ d / dθ ( Li ) ]

= iR + ω_m i [ d L / dθ ] + ω_m L [ di / dθ ]…. ( 3 )

Angular speed ω_m = dθ / dt ……………………( 4 )

From equation ( 3 ) and ( 4 )

V = iR + ω_m i [ d L / dθ ] + L [ dθ / dt ] [ di / dθ ]

V = iR + ω_m i [ d L / dθ ] + L [ di / dt ]

V = iR + L [ di / dt ] + ω_m i [ d L / dθ ] ……..( 5 )

Where

iR = Resistance drop

L [ di / dt ] = Inductance drop

ω_m i [ d L / dθ ] = Back emf or Induced emf

You may also like to read these articles :

Construction of AC Servo Motor

Concentrated Solar Thermal Power

What is Inductor & Inductance?

Types of Filter Circuit

Torque Equation of Switched Reluctance Motor

Voltage Equation of SRM

V = iR + L [ di / dt ] + ω_m i [ d L / dθ ]

Electrical power P = Vi

P = i²R + Li [ di / dt ] + ω_m i² [ d L / dθ ] ….. ( 6 )

Rate of change of magnetic energy

Energy stored in the inductance e = ½ Li²

Rate of change of magnetic energy

d / dt ( ½ Li²)

= ½ i² ( dL / dt ) + ½ L ( 2i di/dt )

= ½ [ i² ( dL / dt ) + L ( 2i di/dt ) ]

= ½ [ i² ( dL / dt ) + 2Li ( di/dt ) ]

= ½ i² ( dL / dt ) + Li ( di/dt )

= ½ i² ( dL / dθ ) ( dθ / dt ) + Li ( di/dt )

= ½ i² ω_m ( dL / dθ ) + Li ( di/dt ) …… ( 7 ) [ ⸫ ω_m = dθ / dt ]

According to principle of Energy Conservation

Mechanical output power P_m = Electrical Input Power – Drop in Resistance – Rate of change of magnetic energy

P_m = i²R + Li [ di / dt ] + ω_m i² [ d L / dθ ]

– ( i²R )

– ( ½ i² ω_m ( dL / dθ ) + Li ( di/dt )

P_m = ½ ω_m i² [ d L / dθ ]

Torque ( T_m ) = P_m / ω_m

= ½ ω_m i² [ d L / dθ ] / ½ i² [ d L / dθ ]

Where ω_m = ½ i² [ d L / dθ ]

Torque ( T_m ) = ½ i² [ d L / dθ ]

Where d L/dθ = Slope of Inductance

Therefore torque = ½ i²( Slope of Inductance )

Pages

15/12/2021

Construction & Working of Switch Reluctance Motor