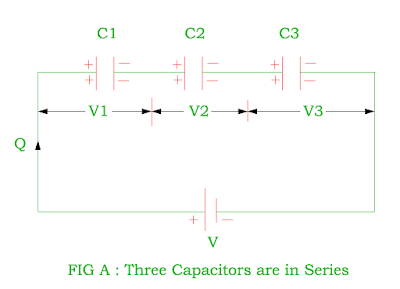
Capacitor in series
- If the positive plate of one capacitor is connected to negative plate of another capacitor , it is called as series connection of capacitors.
- If there are three capacitors connected across direct supply voltage V, same electrons flows through all capacitors therefore charge passes through each capacitor must be same.
- We can say that when capacitors are connected in series, each capacitor get same charge.
- Let the potential difference between three capacitor C1, C2 and C3 are V1, V2 and V3 respectively.
Also
- Charge of capacitor Q = Q1 = Q2 = Q3
Q = CV = C1V1 =
C2V2 = C3V3
Therefore V1 = Q
/ C1
V2 = Q / C2
V3 = Q / C3
- Potential across three capacitors
V = V1 + V2 + V3
Q / C = Q / C1 +
Q / C2 + Q / C3
1 / C = 1 / C1 +
1 / C2 + 1 / C3
- We can say that when the capacitors are connected in series, there equivalent reciprocal of capacitor is equal to sum of reciprocal of their individual capacitors.
Capacitor
in Parallel
- If all the positive plates of the capacitor is connected to positive end of supply and negative plates of the capacitor is connected to negative end of the supply, it is called as parallel connection of capacitors.
- If there are three capacitors connected across direct supply voltage V, the voltage across each capacitor must be same.
- However the charge passes through each capacitor is different.
- Let us consider that the three capacitor C1, C2 and C3 are connected across supply voltage V.
- Let the
charge passes through three capacitors C1, C2 and C3 is Q1, Q2 and Q3
respectively and through supply voltage V is Q.
- Total charge Q = Q1 + Q2 + Q3
CV = C1V + C2V + C3V
C = C1 + C2 + C3
- We can say that when the capacitors are connected in parallel, there equivalent capacitor is sum of all individual capacitors.
You may also like :