- The term torque means ‘Turning movement of the force about an axis.’
T = F × r Newton
– meter
Where T = Torque
F = Force in Newton
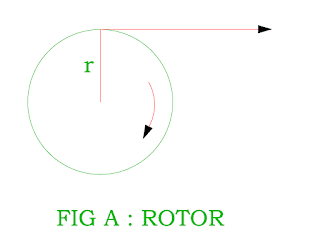
- Consider an armature of radius r meter and force F newton acts on it.
- Let us assume that the armature rotate at speed of N rpm.
- When the armature rotates one revolution, it cuts distance 2πr in time of 60 / N second. Therefore the work done per revolution
= Force ×
distance
= F × 2πr
But F × r = T
- So the work – done / revolution = 2πT Newton – meter
- Now the Power developed
= 2πT / ( 60 / N
)
= 2πNT / 60
= Tω
Where ω =
Angular velocity in radian / second
= 2πN / 60
- The electrical equivalent to mechanical power developed by the armature is given by
T = ( 60 / 2πN )
EbIa …………….( 1 )
| T = 9.55 ( EbIa / N ) |
If the speed is given in revolution per second ( rps )
T = ( 9.55 / 60 ) ( EbIa / N )
|
- T = 0.159 ( EbIa / N )
- As the back emf Eb = ФZNP / 60A
T = ( 60 / 2πN )
( ФZNP / 60A ) Ia
= ( 1 / 2π ) ( ФZNP / A ) Ia N –
m
= [ 1
/ ( 2π × 9.81 ) ] ( ФZNP / A ) Ia Kg – m
- The number of conductor Z, number of poles P and number of parallel paths A is constant in the DC motor therefore
T α ФIa
Shaft
Torque
- The shaft torque Tsh always less than the armature torque due to small amount of friction losses in the motor.
Shaft torque =
Armature torque – Friction and windage losses
Tsh =
Ta – Friction and windage losses
Output
power
- Output power = Power developed in the armature
- The mechanical power develops at the shaft of the DC motor is always less than the armature power due to friction and windage losses.
Psh =
Tsh × ( 2πNT / 60 ) Watt
- The mechanical power developed at the shaft is called as brake horse power ( BHP ).
One HP = 735.5
watt
Psh =
( Tsh × 2πN / 60 )( 1 / 735.5
) HP
You may also like :







electric motor
ReplyDeleteBuy electric water pump motor and three-phase induction motor at an affordable price. Also, we will give you a squirrel cage induction motor and a single phase induction motor.
Contact us *
• Email - info@latteysindustries.com
• Phone number - +91 7861813632